> Übersicht

Verteilung von Datenwerten

Verteilungstyp   Streuung

Physiologische und medizinische Meßwerte unterliegen einer gewissen Streuung. Diese hat mehrere Ursachen. Um zu entscheiden, ob die Ausprägung (Meßwert) eines Merkmals (z.B. Blutdruck) eines Merkmalsträgers (Proband, Patient) als 'normal' (physiologisch) oder 'abnorm' (pathologisch) einzustufen ist, bedarf es einiger Überlegungen.
Merkmale können qualitativ (ohne zahlenmäßige Ordnung, z.B. männlich / weiblich) oder quantitativ sein; und letztere

• diskret (Wertebereich: natürliche Zahlen, z.B. Leukozytenzahl) oder
• stetig (Wertebereich: reelle Zahlen, d.h. auf einer kontinuierlichen Skala liegend, z.B. Betrag des Blutdrucks).

Je nach Art der Merkmale differiert die Darstellung der vorliegenden Verteilung, und werden unterschiedliche statistische Verfahren angewendet.

Verteilungstyp

Ein wichtiger Aspekt für die Angebrachtheit eines Tests ist, wie die Ausprägung in einem bestimmten Kollektiv verteilt ist (z.B. wie verhält sich der Blutdruck unter welchen Umständen bei anderen Merkmalsträgern?). Um diese Frage zu beantworten, können umfangreiche Beobachtungsreihen notwendig sein.

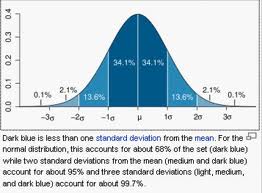
Stetige Merkmale können in einer Gruppe symmetrisch um einen Mittelwert verteilt sein (sog. Gauß-Verteilung, - 'Glockenform' der Funktion der Wahrscheinlichkeitsdichte), oder 'schief' (läßt sich durch Logarithmieren symmetrisch machen), oder auch mehrgipflig (dann verbergen sich mehr als eine 'Population' in der gepoolten Gruppe der Merkmalsträger) - Beispiel: Verteilung der Erythrozyten-Durchmesser (sog. Price-Jones-Kurve).

Sind beim zugrundeliegenden Meßvorgang keine systematischen, sondern nur zufällige Fehler unterlaufen, so gilt für den einzelnen Meßwert:

• Meßwert = wahrer Wert + Zufallsfehler (Gauss-sches Modell).

Die wichtigste theoretische Verteilung ist die 'Normalverteilung' ('normal' als mathematisches Kriterium gemeint).

Wenn über den Verteilungstyp eines Merkmals keine Vorkenntnisse vorliegen und eine Datenauswertung vorgenommen werden soll, deren gültige Anwendung 'Normalität' voraussetzt, muß  zunächst diese Voraussetzung überprüft werden.

Bei wachsendem Stichprobenumfang neigen wichtige aggregierte Werte - wie der Mittelwert - dazu, auch dann normalverteilt zu werden, wenn die Meßgrößen selbst nicht normalverteilt sind. Die Anwendung von Verfahren schließender Statistik, die von Normalität der Verteilung ausgehen, kann dann auch in solchen Fällen sinnvoll sein.

Streuung

Die Streuung metrischer Datenwerte kann unterschiedlich charakterisiert werden: z.B.

• durch den beobachteten Streubereich (Spannweite oder Variationsbreite, engl. range; von Maximal- bis Minimalwert), was extremen Ausreißern hohes Gewicht verleiht;
• durch Angabe von Perzentilenbereichen (z.B. 0-10%, 11-20% etc., wobei 100% der gesamte Bereich ist), oder Quartilabständen, die jeweils 1/4 aller (rangmäßig geordneten) beobachtenen Werte umfassen;
• die Varianz, definiert als die Summe der Quadrate der Abweichungen aller Einzelwerte vom Mittelwert, dividiert durch die Anzahl der 'Freiheitsgrade' (=die um 1 reduzierte Zahl der Einzelbeobachtungen);
• die Standardabweichung (standard deviation, SD), definiert als die Quadratwurzel aus der Varianz;
• der mittlere Fehler der Mittelwerte (standard error of means - SEM), das ist SD dividiert durch die Quadratwurzel der Zahl der Einzelbeobachtungen;
• der Variationskoeffizient, definiert als SD dividiert durch den (arithmetischen) Mittelwert der Verteilung.

©  Helmut Hinghofer-Szalkay