Fehler und Diagnose

Wahrheitsgehalt von Hypothesen und Fehler 1. und 2. Art

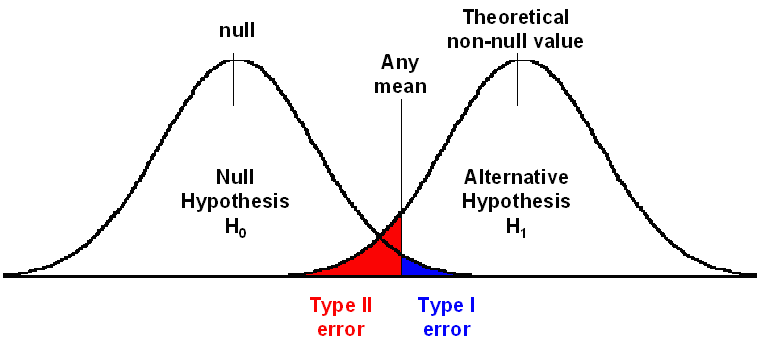
Statistische Tests geben an, wie wahrscheinlich ein vermuteter Sachverhalt zutrifft bzw. eine Nullhypothese zurückgewiesen werden kann. Solche Überlegungen treffen auch auf die Beschreibung der Güte diagnostischer Tests zu. Es können zwei Arten von Fehlern unterlaufen:

Fehler 1. Art (alpha-Fehler): Die zufällige Zusammenstellung der Stichproben kann dazu veranlassen, die Nullhypothese zu verwerfen, obwohl sie in Wirklichkeit richtig ist (z.B. wird vermutet, daß ein Mittel XYZ gegen Bluthochdruck wirksam ist, obwohl die beiden Testgruppen sich in Wahrheit blutdruckmäßig nicht unterscheiden). Die Höhe dieser Irrtumswahrscheinlichkeit nennt man das alpha-Risiko (man spricht auch vom Signifikanzniveau alpha - s. Biometrie). Man sagt auch, die Entscheidung ist bei Unterlaufen eines alpha-Fehlers falsch positiv. Auf eine medizinische Diagnose bezogen, heißt das: man geht von einem positiven Befund aus (Beispiel: Patient krank), obwohl dies unzutreffend ist. Eine diagnostische Methode mit einem hohen alpha-Fehler schlägt also relativ oft 'Alarm', obwohl der Patient in Wahrheit nicht als krank einzustufen wäre. Nach dem Bayes'-Theorem wird unter der Spezifität die Wahrscheinlichkeit verstanden, mit welcher der Test in der Gesamtheit der objektiv nicht kranken Untersuchten auch ein negatives Testergebnis anzeigt. Tests mit hoher Spezifität haben einen geringen Fehler 1. Art.

Fehler 2. Art (beta-Fehler): Die zufällige Zusammenstellung der Stichproben kann dazu veranlassen, die Nullhypothese beizubehalten, obwohl sie in Wirklichkeit falsch ist (z.B. wird vermutet, daß ein Mittel XYZ gegen Bluthochdruck unwirksam ist, obwohl die beiden Testgruppen sich in Wahrheit blutdruckmäßig unterscheiden). Die Höhe dieser Irrtumswahrscheinlichkeit nennt man das beta-Risiko. Man sagt auch, die Entscheidung ist bei Unterlaufen eines beta-Fehlers falsch negativ. Auf eine medizinische Diagnose bezogen, heißt das: die diagnostische Methode findet nichts (klinischer Jargon: 'ohne Befund' - o.B.), obwohl der Patient objektiv als krank einzustufen wäre. Eine Methode mit einem hohen beta-Fehler ist also diagnostisch recht unempfindlich. Nach dem Bayes'-Theorem wird unter der Sensitivität die Wahrscheinlichkeit verstanden, mit welcher der Test in der Gesamtheit der objektiv kranken Untersuchten auch ein positives Testergebnis anzeigt. Tests mit hoher Sensitivität haben einen geringen Fehler 2. Art.

Man kann diesen Zusammenhang auch an folgendem Beispiel demonstrieren: Lautet die Aufgabe, zwischen ausreichend und ungenügend vorbereiteten Kandidaten zu unterscheiden, findet ein 'milder' Prüfer nur wenige schwarze Schafe (großer Fehler 2. Art). Ein 'strenger' Prüfer hingegen wird auch Kandidaten zur Wiederholung bitten, die in Wahrheit ausreichende Kenntnisse hätten (großer Fehler 1. Art).

Populationen, die sich im zu erschließenden Zustand unterscheiden, überschneiden sich in Hinblick auf die Meßgröße (diagnostischer Test, Prüfungsergebnis,..). Man kann die Fehlerwahrscheinlichkeit 2. Art durch Vergrößerung des Stichprobenumfangs zwar verringern, aber das verursacht einen steigenden Aufwand (größere Kosten).

Es geht also um den erwarteten Nutzen eines diagnostischen Tests. Dabei ist zu beachten, dass die diagnostische Aussage naturgemäß nie 'sicher', sondern nur wahrscheinlich sein kann. Der Arzt 'weiß' daher auch nicht über das Schicksal eines Patienten Bescheid, sondern kann nur mehr oder weniger begründete Vermutungen anstellen. Es wäre falsch, einer diagnostischen Methode in dem Sinne zu 'vertrauen', daß sie 'objektive', 'absolute' Resultate liefert, wie dies im medizinischen Alltag leider allzu häufig postuliert wird. Unbedingt müssen Prinzipien der Statistik, der physiologische Gesamtzusammenhang, und die persönlichen Komponenten des Einzelfalls Berücksichtigung finden.